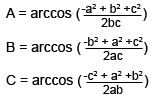Difference between revisions of "Trigonometry Functions"
imported>DragoonWraith |
imported>DragoonWraith |
||
| (13 intermediate revisions by 4 users not shown) | |||
| Line 38: | Line 38: | ||
== Galsiah Version == | == Galsiah Version == | ||
Galsiah says that this version of sine/cosine approximation is faster and more accurate than the Taylor series. (For source, see [http://www.convertit.com/Go/EducationPlanet/Reference/AMS55.ASP?Res=150&Page=76 Handbook of Mathematical Functions].) | |||
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | ||
float ang (the measure of the angle) | float ang ;(the measure of the angle) | ||
float n (used internally) | float n ;(used internally) | ||
float t2 (used internally) | float t2 ;(used internally) | ||
float sin (sine of the angle) | float sin ;(sine of the angle) | ||
float cos (cosine of the angle) | float cos ;(cosine of the angle) | ||
float tan (tangent of the angle) | float tan ;(tangent of the angle) | ||
You may rename these if you wish, but that means changing the code to match. All of them must be floats. | You may rename these if you wish, but that means changing the code to match. All of them must be floats. | ||
| Line 66: | Line 68: | ||
set Wiki.t2 to (Wiki.ang * Wiki.ang) | set Wiki.t2 to (Wiki.ang * Wiki.ang) | ||
set Wiki.sin to (Wiki.ang*(1 - | set Wiki.sin to Wiki.n*(Wiki.ang*(1 - Wiki.t2*0.16605 + 0.00761*Wiki.t2*Wiki.t2)) | ||
set Wiki. | set Wiki.cos to Wiki.n*(1 - Wiki.t2*0.4967 + 0.03705*Wiki.t2*Wiki.t2) | ||
set Wiki.tan to (Wiki.sin/Wiki.cos)</pre> | |||
set Wiki. | |||
For working example (with somewhat simpler code), see [[Summon Object]]. | |||
== Taylor Series Variant 1 == | == Taylor Series Variant 1 == | ||
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | ||
float ang (the measure of the angle) | float ang ;(the measure of the angle) | ||
float rad (used internally) | float rad ;(used internally) | ||
float exp (used internally) | float exp ;(used internally) | ||
float sin (the sine of the angle) | float sin ;(the sine of the angle) | ||
float cos (the cosine of the angle) | float cos ;(the cosine of the angle) | ||
float tan (the tangent of the angle) | float tan ;(the tangent of the angle) | ||
You may rename these if you wish, but that means changing the code, which is not advised, as there are a lot of variables here. All of them must be floats. | You may rename these if you wish, but that means changing the code, which is not advised, as there are a lot of variables here. All of them must be floats. | ||
| Line 96: | Line 96: | ||
set Wiki.rad to ( Wiki.ang * 0.0174533 ) | set Wiki.rad to ( Wiki.ang * 0.0174533 ) | ||
set Wiki.cos to 1 | set Wiki.cos to 1 | ||
set Wiki.exp to Wiki.rad | set Wiki.exp to Wiki.rad ; 1st | ||
set Wiki.sin to Wiki.exp | set Wiki.sin to Wiki.exp | ||
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 2nd | set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 2nd | ||
| Line 124: | Line 124: | ||
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | ||
float angle (measure of the angle) | float angle ;(measure of the angle) | ||
float t1 (used internally) | float t1 ;(used internally) | ||
float t2 (used internally) | float t2 ;(used internally) | ||
float t5 (used internally) | float t5 ;(used internally) | ||
float t6 (used internally) | float t6 ;(used internally) | ||
float sina (sine of the angle) | float sina ;(sine of the angle) | ||
float cosa (cosine of the angle) | float cosa ;(cosine of the angle) | ||
float tana (tangent of the angle) | float tana ;(tangent of the angle) | ||
All must be floats. Though they can be renamed, doing so means changing the function code to match. | All must be floats. Though they can be renamed, doing so means changing the function code to match. | ||
; script originally by JOG | ; script originally by JOG | ||
| Line 141: | Line 141: | ||
set Wiki.t5 to Wiki.t2*Wiki.t2*Wiki.t1 | set Wiki.t5 to Wiki.t2*Wiki.t2*Wiki.t1 | ||
set Wiki.t6 to Wiki.t5*Wiki.t1 | set Wiki.t6 to Wiki.t5*Wiki.t1 | ||
set Wiki.sina to Wiki.t1 - Wiki.t1*Wiki.t2/6 + Wiki.t5/120 - Wiki.t5*t2/5040 + Wiki.t6*Wiki.t2*Wiki.t1/362880 | set Wiki.sina to Wiki.t1 - Wiki.t1*Wiki.t2/6 + Wiki.t5/120 - Wiki.t5*t2/5040 | ||
set Wiki.sina to Wiki.sina + Wiki.t6*Wiki.t2*Wiki.t1/362880 | |||
;note that the previous two lines have been split in order to display properly | |||
;they should be on one line in your code | |||
set Wiki.cosa to 1 - Wiki.t2/2 + Wiki.t2*Wiki.t2/24 - Wiki.t6/720 + Wiki.t6*Wiki.t2/40320 | set Wiki.cosa to 1 - Wiki.t2/2 + Wiki.t2*Wiki.t2/24 - Wiki.t6/720 + Wiki.t6*Wiki.t2/40320 | ||
set Wiki.tana to Wiki.sina/Wiki.cosa | set Wiki.tana to Wiki.sina/Wiki.cosa | ||
| Line 159: | Line 162: | ||
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]: | ||
float x (the sine of the angle) | float x ;(the sine of the angle) | ||
float n (used internally) | float n ;(used internally) | ||
float arcsinx (the arcsine, that is, the measure of the angle) | float arcsinx ;(the arcsine, that is, the measure of the angle) | ||
These may be renamed, but doing so means changing them in the code. | These may be renamed, but doing so means changing them in the code. | ||
| Line 173: | Line 176: | ||
set Wiki.n to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 | set Wiki.n to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 | ||
set arcsinx to 57.2957795*(1.5707963-Wiki.n*(1.5707288-0.2121144*Wiki.x+0.0742610*Wiki.x*Wiki.x-0.0187293*Wiki.x*Wiki.x*Wiki.x)) | set Wiki.arcsinx to 57.2957795*(1.5707963-Wiki.n*(1.5707288-0.2121144*Wiki.x+0.0742610*Wiki.x*Wiki.x-0.0187293*Wiki.x*Wiki.x*Wiki.x)) | ||
;note that this does not display properly - be sure to get the entire line with copy and paste | |||
This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations. | This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations. | ||
| Line 184: | Line 188: | ||
This can be approximated by Oblivion using a [[:Category:Staged Functions|function]]. This function requires the following variables be declared in your [[Global Script]]: | This can be approximated by Oblivion using a [[:Category:Staged Functions|function]]. This function requires the following variables be declared in your [[Global Script]]: | ||
float z (the sine of the angle) | float z ;(the sine of the angle) | ||
float z3 (used internally) | float z3 ;(used internally) | ||
float z5 (used internally) | float z5 ;(used internally) | ||
float z7 (used internally) | float z7 ;(used internally) | ||
float arcsinz (the arcsine, that is, the measure of the angle) | float arcsinz ;(the arcsine, that is, the measure of the angle) | ||
These can be renamed, but must also be changed in the code. | These can be renamed, but must also be changed in the code. | ||
;script originally by DragoonWraith | ;script originally by DragoonWraith | ||
| Line 195: | Line 199: | ||
set Wiki.z7 to (Wiki.z5*Wiki.z*Wiki.z) | set Wiki.z7 to (Wiki.z5*Wiki.z*Wiki.z) | ||
set arcsinz to (Wiki.z+(1/2)*(Wiki.z3/3)+(3/8)*(Wiki.z5/5)+(15/48)*(Wiki.z7/7)) | set Wiki.arcsinz to (Wiki.z+(1/2)*(Wiki.z3/3)+(3/8)*(Wiki.z5/5)+(15/48)*(Wiki.z7/7)) | ||
More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit. | More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit. | ||
| Line 202: | Line 206: | ||
See above for method of obtaining arcsin. This may be useful when using the Law of Cosines to find the measure of an unknown angle, given three known sides. | See above for method of obtaining arcsin. This may be useful when using the Law of Cosines to find the measure of an unknown angle, given three known sides. | ||
<b><u>Law of Cosines</u></b> | |||
<i>a</i><sup>2</sup> = <i>b</i><sup>2</sup> + <i>c</i><sup>2</sup> - 2<i>bc</i> cos<i>A</i> | |||
<i>b</i><sup>2</sup> = <i>a</i><sup>2</sup> + <i>c</i><sup>2</sup> - 2<i>bc</i> cos<i>B</i> | |||
j<i>c</i><sup>2</sup> = <i>a</i><sup>2</sup> + <i>b</i><sup>2</sup> - 2<i>ab</i> cos<i>C</i> | |||
That is, the square of one side is equal to the sum of the other squares of the other two, minus twice the product of the other two sides with the cosine of the angle opposite that side. | |||
Simple algebra gives the following equations for any given angle in a triangle, if you know the lengths of all three sides. | |||
[[Image:LawOfCosinesForAngle.png]] | |||
= Arctangent = | = Arctangent = | ||
| Line 209: | Line 227: | ||
This function requires the following variables be declared in your [[Global Script]]: | This function requires the following variables be declared in your [[Global Script]]: | ||
float z (the tangent of the angle) | float z ;(the tangent of the angle) | ||
float z3 (used internally) | float z3 ;(used internally) | ||
float z5 (used internally) | float z5 ;(used internally) | ||
float z7 (used internally) | float z7 ;(used internally) | ||
float | float arctanz ;(the arctangent, that is, the measure of the angle) | ||
These can be renamed, but must also be changed in the code. | These can be renamed, but must also be changed in the code. | ||
;modified from arcsine script supplied by DragoonWraith | ;modified from arcsine script supplied by DragoonWraith | ||
set z3 to ( z * z * z ) | set Wiki.z3 to ( Wiki.z * Wiki.z * Wiki.z ) | ||
set z5 to ( z3 * z * z ) | set Wiki.z5 to ( Wiki.z3 * Wiki.z * Wiki.z ) | ||
set z7 to ( z5 * z * z ) | set Wiki.z7 to ( Wiki.z5 * Wiki.z * Wiki.z ) | ||
set arctanz to ( z - (z3/3) + (z5/5) - (z7/7) ) | set Wiki.arctanz to ( Wiki.z - (Wiki.z3/3) + (Wiki.z5/5) - (Wiki.z7/7) ) | ||
Again, more terms equals more accuracy. | Again, more terms equals more accuracy. | ||
| Line 229: | Line 247: | ||
[http://www.elderscrolls.com/forums/index.php?showtopic=410923 Elder Scrolls Forums - Is there an actor for the target you are attacking currently?] | [http://www.elderscrolls.com/forums/index.php?showtopic=410923 Elder Scrolls Forums - Is there an actor for the target you are attacking currently?] | ||
[[Ingame Functions|Ingame Functions (example uses simple (3-line) sin/cos script functions: example for player x-hair)]] | |||
[[Category: Stage Functions]] | [[Category: Stage Functions]] | ||
[[Category: | [[Category: Math Functions (CS 1.0)]] | ||
Latest revision as of 20:19, 25 April 2010
This is a repository of functions used in trigonometry - namely Sine, Cosine, Tangent, Arcsine, Arccosine, and Arctangent.
There are many methods of obtaining any or all of these, and each has its own benefits and drawbacks in terms of length, efficiency, and speed. This page is a work in progress - please add any scripts you have for approximating these functions. Please remember to comment them thoroughly and to use generic variable names.
These are Stage Functions, and as such must be created as Quest Stages of a Global Script and called as a function. These examples assume a Quest called Wiki with the variables declared. Therefore, you must modify this code to include the name of your Quest (assuming it is not Wiki, which it shouldn't be). Any contributors, please read that article and write your code in that format.
Formulae[edit | edit source]
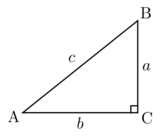
A + B + C = 180°
A + B = 90°
a² + b² = c²
sin(A) = a / c
cos(A) = b / c
tan(A) = a / b
tan(A) = sin(A) / cos(A)
Sine, Cosine, and Tangent[edit | edit source]
You can use a Taylor series to approximate the value of sine, cosine and tangent:
sin(x) = x^1/1! - x^3/3! + x^5/5! - x^7/7! + ...
cos(x) = x^0/0! - x^2/2! + x^4/4! - x^6/6! + ...
tan(x) = x^1/1! + x^3/3! + x^5/5! + x^7/7! + ...
Galsiah Version[edit | edit source]
Galsiah says that this version of sine/cosine approximation is faster and more accurate than the Taylor series. (For source, see Handbook of Mathematical Functions.)
This function requires the following variables to be declared in your Global Script:
float ang ;(the measure of the angle) float n ;(used internally) float t2 ;(used internally) float sin ;(sine of the angle) float cos ;(cosine of the angle) float tan ;(tangent of the angle)
You may rename these if you wish, but that means changing the code to match. All of them must be floats.
;script originally by Galsiah
if Wiki.ang < 0
set Wiki.ang to (Wiki.ang + 360)
elseif Wiki.ang >= 360
set Wiki.ang to (Wiki.ang - 360)
endif
set Wiki.ang to (Wiki.ang/Wiki.rad)
set Wiki.n to 1
if (Wiki.ang > 4.7123)
Set Wiki.ang to (Wiki.ang - 6.2832)
elseif ( Wiki.ang > 1.5708 )
Set Wiki.ang to (Wiki.ang - 3.1416)
Set Wiki.n to -1
endif
set Wiki.t2 to (Wiki.ang * Wiki.ang)
set Wiki.sin to Wiki.n*(Wiki.ang*(1 - Wiki.t2*0.16605 + 0.00761*Wiki.t2*Wiki.t2))
set Wiki.cos to Wiki.n*(1 - Wiki.t2*0.4967 + 0.03705*Wiki.t2*Wiki.t2)
set Wiki.tan to (Wiki.sin/Wiki.cos)
For working example (with somewhat simpler code), see Summon Object.
Taylor Series Variant 1[edit | edit source]
This function requires the following variables to be declared in your Global Script:
float ang ;(the measure of the angle) float rad ;(used internally) float exp ;(used internally) float sin ;(the sine of the angle) float cos ;(the cosine of the angle) float tan ;(the tangent of the angle)
You may rename these if you wish, but that means changing the code, which is not advised, as there are a lot of variables here. All of them must be floats.
; script originally by Galerion
; normalize angle
if ( Wiki.ang < -180 )
set Wiki.ang to ( Wiki.ang + 360 )
elseif ( Wiki.ang > 180 )
set Wiki.ang to ( Wiki.ang - 360 )
endif
; approximate sine and cosine of the angle
set Wiki.rad to ( Wiki.ang * 0.0174533 )
set Wiki.cos to 1
set Wiki.exp to Wiki.rad ; 1st
set Wiki.sin to Wiki.exp
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 2nd
set Wiki.cos to ( Wiki.cos - Wiki.exp / 2 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 3rd
set Wiki.sin to ( Wiki.sin - Wiki.exp / 6 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 4th
set Wiki.cos to ( Wiki.cos + Wiki.exp / 24 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 5th
set Wiki.sin to ( Wiki.sin + Wiki.exp / 120 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 6th
set Wiki.cos to ( Wiki.cos - Wiki.exp / 720 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 7th
set Wiki.sin to ( Wiki.sin - Wiki.exp / 5040 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 8th
set Wiki.cos to ( Wiki.cos + Wiki.exp / 40320 )
set Wiki.exp to ( Wiki.exp * Wiki.rad ) ; 9th
set Wiki.sin to ( Wiki.sin + Wiki.exp / 362880 )
; get tangent
set Wiki.tan to ( Wiki.sin / Wiki.cos )
End
This script is more accurate than it needs to be. Galerion suggests that only the first seven steps are necessary.
Taylor Series Variant 2[edit | edit source]
This function requires the following variables to be declared in your Global Script:
float angle ;(measure of the angle) float t1 ;(used internally) float t2 ;(used internally) float t5 ;(used internally) float t6 ;(used internally) float sina ;(sine of the angle) float cosa ;(cosine of the angle) float tana ;(tangent of the angle)
All must be floats. Though they can be renamed, doing so means changing the function code to match.
; script originally by JOG ; normalize the angle set Wiki.angle to Wiki.angle + 360*(Wiki.angle < -180) - 360*(Wiki.angle > 180) ; precalculate powers of "angle" set Wiki.t1 to Wiki.angle / 57.29577951 set Wiki.t2 to Wiki.t1*Wiki.t1 set Wiki.t5 to Wiki.t2*Wiki.t2*Wiki.t1 set Wiki.t6 to Wiki.t5*Wiki.t1 set Wiki.sina to Wiki.t1 - Wiki.t1*Wiki.t2/6 + Wiki.t5/120 - Wiki.t5*t2/5040 set Wiki.sina to Wiki.sina + Wiki.t6*Wiki.t2*Wiki.t1/362880 ;note that the previous two lines have been split in order to display properly ;they should be on one line in your code set Wiki.cosa to 1 - Wiki.t2/2 + Wiki.t2*Wiki.t2/24 - Wiki.t6/720 + Wiki.t6*Wiki.t2/40320 set Wiki.tana to Wiki.sina/Wiki.cosa
Arcsine[edit | edit source]
Arcsine[edit | edit source]
Sin=Opp/Hyp - The arcsine is the angle between two points, when the distance is the hypotenuse of the triangle and the opposing side is either the x- or the y-difference (whatever is shorter). To get the z-angle (left/right) between two objects in Oblivion you can use the function GetHeadingAngle. But when you need the x-angle (up/down) you still have to calculate the arcsin.
Abramowitz/Stegun Approximation[edit | edit source]
Abramowitz and Stegun found this polynomal approximation for arcsine:
a0=1.5707288 / a1=-0.2121144 / a2=0.0742610 / a3=-0.0187293
arcsin(x) = 180/Pi * (pi/2 - sqrt(1 - x) * (a0 + a1*x + a2*x^2 + a3*x^3))
This function requires the following variables to be declared in your Global Script:
float x ;(the sine of the angle) float n ;(used internally) float arcsinx ;(the arcsine, that is, the measure of the angle)
These may be renamed, but doing so means changing them in the code.
; script originally by JOG set Wiki.x to (player.getpos z - NPC.getpos z)/player.getdistance NPC set Wiki.n to 1 - Wiki.x ; arcsinx = SquareRoot(1-x) set Wiki.arcsinx to Wiki.n/2 set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 set Wiki.n to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2 set Wiki.arcsinx to 57.2957795*(1.5707963-Wiki.n*(1.5707288-0.2121144*Wiki.x+0.0742610*Wiki.x*Wiki.x-0.0187293*Wiki.x*Wiki.x*Wiki.x)) ;note that this does not display properly - be sure to get the entire line with copy and paste
This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations.
Approximation by Taylor Series[edit | edit source]
According to Wikipedia, arcsine can be found with this series:
This can be approximated by Oblivion using a function. This function requires the following variables be declared in your Global Script:
float z ;(the sine of the angle) float z3 ;(used internally) float z5 ;(used internally) float z7 ;(used internally) float arcsinz ;(the arcsine, that is, the measure of the angle)
These can be renamed, but must also be changed in the code.
;script originally by DragoonWraith set Wiki.z3 to (Wiki.z*Wiki.z*Wiki.z) set Wiki.z5 to (Wiki.z3*Wiki.z*Wiki.z) set Wiki.z7 to (Wiki.z5*Wiki.z*Wiki.z) set Wiki.arcsinz to (Wiki.z+(1/2)*(Wiki.z3/3)+(3/8)*(Wiki.z5/5)+(15/48)*(Wiki.z7/7))
More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit.
Arccosine[edit | edit source]
Arccos z = (PI / 2) - arcsin(z).
See above for method of obtaining arcsin. This may be useful when using the Law of Cosines to find the measure of an unknown angle, given three known sides.
Law of Cosines
a2 = b2 + c2 - 2bc cosA
b2 = a2 + c2 - 2bc cosB
jc2 = a2 + b2 - 2ab cosC
That is, the square of one side is equal to the sum of the other squares of the other two, minus twice the product of the other two sides with the cosine of the angle opposite that side.
Simple algebra gives the following equations for any given angle in a triangle, if you know the lengths of all three sides.
Arctangent[edit | edit source]
Arctan z = z - (z^3/3) + (z^5/5) - (z^7/7) +...
This is very similar to the Taylor Expansion method of generating Arcsine, but without the extra multipliers, and with alternating signs.
This function requires the following variables be declared in your Global Script:
float z ;(the tangent of the angle) float z3 ;(used internally) float z5 ;(used internally) float z7 ;(used internally) float arctanz ;(the arctangent, that is, the measure of the angle)
These can be renamed, but must also be changed in the code.
;modified from arcsine script supplied by DragoonWraith set Wiki.z3 to ( Wiki.z * Wiki.z * Wiki.z ) set Wiki.z5 to ( Wiki.z3 * Wiki.z * Wiki.z ) set Wiki.z7 to ( Wiki.z5 * Wiki.z * Wiki.z ) set Wiki.arctanz to ( Wiki.z - (Wiki.z3/3) + (Wiki.z5/5) - (Wiki.z7/7) )
Again, more terms equals more accuracy.
See Also[edit | edit source]
Elder Scrolls Forums - Trigonometry Function Workarounds?
Elder Scrolls Forums - Is there an actor for the target you are attacking currently?
Ingame Functions (example uses simple (3-line) sin/cos script functions: example for player x-hair)