Difference between revisions of "Trigonometry Functions"

From the Oblivion ConstructionSet Wiki
Jump to navigation Jump to search
imported>JOG
imported>DragoonWraith
(changed to stage functions)
Line 3: Line 3:
There are many methods of obtaining any or all of these, and each has its own benefits and drawbacks in terms of length, efficiency, and speed. This page is a work in progress - please add any scripts you have for approximating these functions. Please remember to comment them thoroughly and to use generic variable names.
There are many methods of obtaining any or all of these, and each has its own benefits and drawbacks in terms of length, efficiency, and speed. This page is a work in progress - please add any scripts you have for approximating these functions. Please remember to comment them thoroughly and to use generic variable names.


These are [[:Category:Stage_Functions|Stage Functions]], and as such must be created as [[Quest Stages Tab|Quest Stages]] of a [[Global Script]] and called as a function. These examples assume a [[Quest]] called Wiki with the variables declared. Therefore, you must modify this code to include the name of your [[Quest]] (assuming it is not Wiki, which it shouldn't be).


= Formulae =
= Formulae =
Line 36: Line 37:
'''''tan(x) = x^1/1! + x^3/3! + x^5/5! + x^7/7! + ...'''''
'''''tan(x) = x^1/1! + x^3/3! + x^5/5! + x^7/7! + ...'''''


== Taylor Series Variant 1 ==  
== Taylor Series Variant 1 ==
  ScriptName SineCosineTangent
 
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]:
  float ang (the measure of the angle)
float rad (used internally)
float exp (used internally)
float sin (the sine of the angle)
float cos (the cosine of the angle)
float tan (the tangent of the angle)
You may rename these if you wish, but that means changing the code, which is not advised, as there are a lot of variables here. All of them must be floats.
 
  ; script originally by Galerion
  ; script originally by Galerion
float ang
float rad
float cos
float sin
float tan
float exp
Begin {appropriate blocktype}
; how one sets ang depends on implementation. Here it is the player's Z rotation
  set ang to Player.GetAngle Z
  ; normalize angle
  ; normalize angle
   if ( ang < -180 )
   if ( Wiki.ang < -180 )
     set ang to ( ang + 360 )
     set Wiki.ang to ( Wiki.ang + 360 )
   elseif ( ang > 180 )
   elseif ( Wiki.ang > 180 )
     set ang to ( ang - 360 )
     set ang to ( Wiki.ang - 360 )
   endif
   endif
   
   
  ; approximate sine and cosine of the angle
  ; approximate sine and cosine of the angle
   set rad to ( ang * 0.0174533 )
   set Wiki.rad to ( Wiki.ang * 0.0174533 )
   set cos to 1
   set Wiki.cos to 1
   set exp to rad                    ; 1st
   set Wiki.exp to Wiki.rad                    ; 1st
   set sin to exp
   set Wiki.sin to Wiki.exp
   set exp to ( exp * rad )          ; 2nd
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 2nd
   set cos to ( cos - exp / 2 )
   set Wiki.cos to ( Wiki.cos - Wiki.exp / 2 )
   set exp to ( exp * rad )          ; 3rd
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 3rd
   set sin to ( sin - exp / 6 )
   set Wiki.sin to ( Wiki.sin - Wiki.exp / 6 )
   set exp to ( exp * rad )          ; 4th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 4th
   set cos to ( cos + exp / 24 )
   set Wiki.cos to ( Wiki.cos + Wiki.exp / 24 )
   set exp to ( exp * rad )          ; 5th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 5th
   set sin to ( sin + exp / 120 )
   set Wiki.sin to ( Wiki.sin + Wiki.exp / 120 )
   set exp to ( exp * rad )          ; 6th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 6th
   set cos to ( cos - exp / 720 )
   set Wiki.cos to ( Wiki.cos - Wiki.exp / 720 )
   set exp to ( exp * rad )          ; 7th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 7th
   set sin to ( sin - exp / 5040 )
   set Wiki.sin to ( Wiki.sin - Wiki.exp / 5040 )
   set exp to ( exp * rad )          ; 8th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 8th
   set cos to ( cos + exp / 40320 )
   set Wiki.cos to ( Wiki.cos + Wiki.exp / 40320 )
   set exp to ( exp * rad )          ; 9th
   set Wiki.exp to ( Wiki.exp * Wiki.rad )          ; 9th
   set sin to ( sin + exp / 362880 )
   set Wiki.sin to ( Wiki.sin + Wiki.exp / 362880 )
   
   
  ; get tangent
  ; get tangent
   set tan to ( sin / cos )
   set Wiki.tan to ( Wiki.sin / Wiki.cos )
   
   
  End
  End
This can be placed within your own code or run as a separate script and checked by yours (though the former is probably easier). The sin, cos, and tan variables are your outputs, ang is your input.
This script is more accurate than it needs to be. Galerion suggests that only the first seven steps are necessary.
This script is more accurate than it needs to be. Galerion suggests that only the first seven steps are necessary.




== Taylor Series Variant 2 ==  
== Taylor Series Variant 2 ==  
  ScriptName SineCosineTangent
 
This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]:
  float angle (measure of the angle)
float t1 (used internally)
float t2 (used internally)
float t5 (used internally)
float t6 (used internally)
float sina  (sine of the angle)
float cosa  (cosine of the angle)
float tana  (tangent of the angle)
All must be floats. Though they can be renamed, doing so means changing the function code to match.
  ; script originally by JOG
  ; script originally by JOG
   
  ; normalize the angle
float angle ; Input
  set Wiki.angle to Wiki.angle + 360*(Wiki.angle < -180) - 360*(Wiki.angle > 180)
float sina  ; Output Sin
; precalculate powers of "angle"
float cosa  ; Output Cos
set Wiki.t1 to Wiki.angle / 57.29577951
  float tana  ; Output Tan
set Wiki.t2 to Wiki.t1*Wiki.t1
float t1
set Wiki.t5 to Wiki.t2*Wiki.t2*Wiki.t1
float t2
set Wiki.t6 to Wiki.t5*Wiki.t1
float t5
set Wiki.sina to Wiki.t1 - Wiki.t1*Wiki.t2/6 + Wiki.t5/120 - Wiki.t5*t2/5040 + Wiki.t6*Wiki.t2*Wiki.t1/362880  
float t6
set Wiki.cosa to 1 - Wiki.t2/2 + Wiki.t2*Wiki.t2/24 - Wiki.t6/720 + Wiki.t6*Wiki.t2/40320
  set Wiki.tana to Wiki.sina/Wiki.cosa
Begin {appropriate blocktype}
  set angle to player.getangle z
  set angle to angle + 360*(angle < -180) - 360*(angle > 180) ; Normalize
  set t1 to angle / 57.29577951   ; precalculate powers of "angle"
  set t2 to t1*t1
  set t5 to t2*t2*t1
  set t6 to t5*t1
  set sina to t1 - t1*t2/6 + t5/120 - t5*t2/5040 + t6*t2*t1/362880  
  set cosa to 1 - t2/2 + t2*t2/24 - t6/720 + t6*t2/40320
  set tana to sina/cosa
end
 
== Taylor Series Variant 3 ==
The idea here is to approximate sin(z) and cos(z) with taylor. Since taylor works best with values close to 0,
I think it's a good idea to use sin and cos periodicity as many times as possible. then I used taylor to approximate the functions. (Scripts by bifmadeinsabbioni)
ScriptName Sin(Z)
set Angolo to AngleZ ; Angolo is the angle of which we want to calculate the sin
set Sign to 1 ; it's the sign adjustment of the result
if (Angolo < 0) ; sin(-z) = -sin(z)
        set Angolo to Angolo * (-1)
        set Sign to Sign * (-1)
endif
if (Angolo > 180)&& (Angolo <=360) ; if 180<=z<=360 sin(z) = -sin(z-180)
set Sign to Sign * (-1)
set Angolo to (Angolo - 180)
endif
 
  if (Angolo > 90)&&(Angolo <=180) ; if 90<=z<=180 sin (z) = sin (180-z)
set Angolo to (180 - angolo)
endif
if (Angolo >45)&&(Angolo <=90) ; if 45<z<90 sin(z) = cos(90-z)
set Angle to (90 - Angolo)
      set Angle to (3.14159265 * Angle / 180) ;now in radiants
set X2 to Angle * Angle
set X4 to X2 * X2
set X6 to X4 * X2
set X8 to X4 * X4
set SinZ to (1 - X2 / 2 + X4 / 24 - X6 / 720 + X8 / 40320)
set SinZ to SinZ*Sign
endif
if (Angolo>=0)&&(Angolo<=45)
set Angle to Angolo
      set Angle to (3.14159265 * Angle / 180) ;now in radiants
set X to Angle
set X3 to X*X*X
set X5 to X3*X*X
set X7 to X3*X3*X
set X9 to X3*X3*X3
set SinZ to (X - X3 / 6 + X5 / 120 - X7 / 5040 + X9 / 362880)
set SinZ to SinZ*Sign
endif
 
ScriptName Cos(Z)
set Angolo to AngleZ ; Angolo is the angle of which we want to calculate the cos
set Sign to 1 ; it's the sign adjustment of the result
 
if (Angolo < 0) ; cos(-z) = cos(z)
        set Angolo to Angolo * (-1)
endif
if (Angolo > 180)&& (Angolo <=360) ; if 180<=z<=360 cos(z) = -cos(z-180)
set Sign to Sign * (-1)
set Angolo to (Angolo - 180)
endif
if (Angolo > 90)&&(Angolo <=180)  ; if 90<=z<=180 cos (z) = -cos(180-z)
set Angolo to (180 - Angolo)
set Sign to Sign * (-1)
endif
if (Angolo >45)&&(Angolo <=90) if 45<z<90 cos(z) = sin(90-z)
set Angle to (90 - Angolo)
      set Angle to (3.14159265 * Angle / 180) ;now in radiants
set X to Angle
set X3 to X*X*X
set X5 to X3*X*X
set X7 to X3*X3*X
set X9 to X3*X3*X3
set CosZ to (X - X3 / 6 + X5 / 120 - X7 / 5040 + X9 / 362880)
set CosZ to CosZ * Sign
endif
if (Angolo>=0)&&(Angolo<=45)
set Angle to Angolo
      set Angle to (3.14159265 * Angle / 180) ;now in radiants
set X2 to Angle * Angle
set X4 to X2 * X2
set X6 to X4 * X2
set X8 to X4 * X4
set CosZ to (1 - X2 / 2 + X4 / 24 - X6 / 720 + X8 / 40320)
set CosZ to CosZ * Sign
endif
 
= Arcsine, Arccosine, and Arctangent =
 
Sin=Opp/Hyp - The arcsine is the angle between two points, when the distance is the hypotenuse of the triangle and the opposing side is either the x- or the y-difference (whatever is shorter). To get the z-angle (left/right) between two objects in Oblivion you can use the function [[GetHeadingAngle]]. But when you need the x-angle (up/down) you still have to calculate the arcsin.
 


== Arcsine - Abramowitz/Stegun Approximation ==
== Arcsine - Abramowitz/Stegun Approximation ==
Line 213: Line 116:
'''''arcsin(x) = 180/Pi * (pi/2 - sqrt(1 - x) * (a0 + a1*x + a2*x^2 + a3*x^3))'''''
'''''arcsin(x) = 180/Pi * (pi/2 - sqrt(1 - x) * (a0 + a1*x + a2*x^2 + a3*x^3))'''''


This [[:Category:Stage Functions|function]] requires the following variables to be declared in your [[Global Script]]:
float x (the sine of the angle)
float n (used internally)
float arcsinx (the arcsine, that is, the measure of the angle)
These may be renamed, but doing so means changing them in the code.


; script originally by JOG
set Wiki.x to (player.getpos z - NPC.getpos z)/player.getdistance NPC
set Wiki.n to 1 - Wiki.x ; arcsinx = SquareRoot(1-x)
set Wiki.arcsinx to Wiki.n/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.n to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2


  scriptname Arcsine
  set arcsinx to 57.2957795*(1.5707963-Wiki.n*(1.5707288-0.2121144*Wiki.x+0.0742610*Wiki.x*Wiki.x-0.0187293*Wiki.x*Wiki.x*Wiki.x))
; script originally by JOG
   
float x        ; Input  (Sine)
float arcsinx  ; Output (Angle)
float n
Begin {appropriate blocktype}
  set x to (player.getpos z - NPC.getpos z)/player.getdistance NPC
  set n to 1 - x                          ; arcsinx = SquareRoot(1-x)
  set arcsinx to n/2
  set arcsinx to (arcsinx+(n/arcsinx))/2
  set arcsinx to (arcsinx+(n/arcsinx))/2
  set arcsinx to (arcsinx+(n/arcsinx))/2
  set n to (arcsinx+(n/arcsinx))/2
  set arcsinx to 57.2957795*(1.5707963-n*(1.5707288-0.2121144*x+0.0742610*x*x-0.0187293*x*x*x))
End


This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations.
This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations.


== Arcsine - Approximation by Taylor Series ==
== Arcsine - Approximation by Taylor Series ==
Line 243: Line 141:
[[Image:Arcsine.png]]
[[Image:Arcsine.png]]


This can be approximated by Oblivion using the following script:
This can be approximated by Oblivion using a [[:Category:Staged Functions|function]]. This function requires the following variables be declared in your [[Global Script]]:  
 
  float z (the sine of the angle)
scriptname Arcsine
  float z3 (used internally)
;script originally supplied by DragoonWraith
  float z5 (used internally)
  float z7 (used internally)
  float z
  float arcsinz (the arcsine, that is, the measure of the angle)
  float z3
These can be renamed, but must also be changed in the code.
  float z5
  ;script originally by DragoonWraith
  float z7
  set Wiki.z3 to (Wiki.z*Wiki.z*Wiki.z)
  float arcsinz
set Wiki.z5 to (Wiki.z3*Wiki.z*Wiki.z)
   
set Wiki.z7 to (Wiki.z5*Wiki.z*Wiki.z)
  Begin {appropriate blocktype}
   
   
  ;z can be set depending on implementation
  set arcsinz to (Wiki.z+(1/2)*(Wiki.z3/3)+(3/8)*(Wiki.z5/5)+(15/48)*(Wiki.z7/7))
;here it is set to the number of places discovered by the player
;(a completely bizarre thing to find the arcsine of)
  set z to GetPCMiscStat 7
  set z3 to ( z * z * z )
  set z5 to ( z3 * z * z )
  set z7 to ( z5 * z * z )
  set arcsinz to ( z + (1/2)*(z3/3) + (3/8)*(z5/5) + (15/48)*(z7/7) )
End
 
 
More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit.
More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit.


Line 283: Line 168:
This is very similar to the Taylor Expansion method of generating Arcsine, but without the extra multipliers, and with alternating signs.
This is very similar to the Taylor Expansion method of generating Arcsine, but without the extra multipliers, and with alternating signs.


  scriptname Arctan
This function requires the following variables be declared in your [[Global Script]]:
  float z (the tangent of the angle)
float z3 (used internally)
float z5 (used internally)
float z7 (used internally)
float arcsinz (the arctangent, that is, the measure of the angle)
These can be renamed, but must also be changed in the code.
  ;modified from arcsine script supplied by DragoonWraith
  ;modified from arcsine script supplied by DragoonWraith
float z
float z3
float z5
float z7
float arctanz
Begin {appropriate blocktype}
;z can be set depending on implementation
;here it is set to the number of places discovered by the player
;(a completely bizarre thing to find the arcsine of)
  set z to GetPCMiscStat 7
   set z3 to ( z * z * z )
   set z3 to ( z * z * z )
   set z5 to ( z3 * z * z )
   set z5 to ( z3 * z * z )
Line 303: Line 181:
   
   
   set arctanz to ( z - (z3/3) + (z5/5) - (z7/7) )
   set arctanz to ( z - (z3/3) + (z5/5) - (z7/7) )
End


Again, more terms equals more accuracy.
Again, more terms equals more accuracy.
Line 314: Line 190:
[http://www.elderscrolls.com/forums/index.php?showtopic=410923 Elder Scrolls Forums - Is there an actor for the target you are attacking currently?]
[http://www.elderscrolls.com/forums/index.php?showtopic=410923 Elder Scrolls Forums - Is there an actor for the target you are attacking currently?]


[[Category: Stage Functions]]
[[Category: Extra_Math_Functions]]
[[Category: Extra_Math_Functions]]
[[Category: Useful_Code]]

Revision as of 19:45, 9 May 2006

This is a repository of functions used in trigonometry - namely Sine, Cosine, Tangent, Arcsine, Arccosine, and Arctangent.

There are many methods of obtaining any or all of these, and each has its own benefits and drawbacks in terms of length, efficiency, and speed. This page is a work in progress - please add any scripts you have for approximating these functions. Please remember to comment them thoroughly and to use generic variable names.

These are Stage Functions, and as such must be created as Quest Stages of a Global Script and called as a function. These examples assume a Quest called Wiki with the variables declared. Therefore, you must modify this code to include the name of your Quest (assuming it is not Wiki, which it shouldn't be).

Formulae

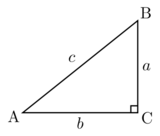
Right triangle

A + B + C = 180°

A + B = 90°

a² + b² = c²

sin(A) = a / c

cos(A) = b / c

tan(A) = a / b

tan(A) = sin(A) / cos(A)



Sine, Cosine, and Tangent

You can use a Taylor series to approximate the value of sine, cosine and tangent:


sin(x) = x^1/1! - x^3/3! + x^5/5! - x^7/7! + ...

cos(x) = x^0/0! - x^2/2! + x^4/4! - x^6/6! + ...

tan(x) = x^1/1! + x^3/3! + x^5/5! + x^7/7! + ...

Taylor Series Variant 1

This function requires the following variables to be declared in your Global Script: 

float ang (the measure of the angle)
float rad (used internally)
float exp (used internally)
float sin (the sine of the angle)
float cos (the cosine of the angle)
float tan (the tangent of the angle)

You may rename these if you wish, but that means changing the code, which is not advised, as there are a lot of variables here. All of them must be floats. 

; script originally by Galerion
; normalize angle
  if ( Wiki.ang < -180 )
    set Wiki.ang to ( Wiki.ang + 360 )
  elseif ( Wiki.ang > 180 )
    set ang to ( Wiki.ang - 360 )
  endif

; approximate sine and cosine of the angle
  set Wiki.rad to ( Wiki.ang * 0.0174533 )
  set Wiki.cos to 1
  set Wiki.exp to Wiki.rad                     ; 1st
  set Wiki.sin to Wiki.exp
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 2nd
  set Wiki.cos to ( Wiki.cos - Wiki.exp / 2 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 3rd
  set Wiki.sin to ( Wiki.sin - Wiki.exp / 6 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 4th
  set Wiki.cos to ( Wiki.cos + Wiki.exp / 24 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 5th
  set Wiki.sin to ( Wiki.sin + Wiki.exp / 120 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 6th
  set Wiki.cos to ( Wiki.cos - Wiki.exp / 720 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 7th
  set Wiki.sin to ( Wiki.sin - Wiki.exp / 5040 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 8th
  set Wiki.cos to ( Wiki.cos + Wiki.exp / 40320 )
  set Wiki.exp to ( Wiki.exp * Wiki.rad )           ; 9th
  set Wiki.sin to ( Wiki.sin + Wiki.exp / 362880 )

; get tangent
  set Wiki.tan to ( Wiki.sin / Wiki.cos )

End

This script is more accurate than it needs to be. Galerion suggests that only the first seven steps are necessary.


Taylor Series Variant 2

This function requires the following variables to be declared in your Global Script: 

float angle (measure of the angle)
float t1 (used internally)
float t2 (used internally)
float t5 (used internally)
float t6 (used internally)
float sina  (sine of the angle)
float cosa  (cosine of the angle)
float tana  (tangent of the angle)

All must be floats. Though they can be renamed, doing so means changing the function code to match. 

; script originally by JOG
; normalize the angle
set Wiki.angle to Wiki.angle + 360*(Wiki.angle < -180) - 360*(Wiki.angle > 180)
; precalculate powers of "angle"
set Wiki.t1 to Wiki.angle / 57.29577951
set Wiki.t2 to Wiki.t1*Wiki.t1
set Wiki.t5 to Wiki.t2*Wiki.t2*Wiki.t1
set Wiki.t6 to Wiki.t5*Wiki.t1
set Wiki.sina to Wiki.t1 - Wiki.t1*Wiki.t2/6 + Wiki.t5/120 - Wiki.t5*t2/5040 + Wiki.t6*Wiki.t2*Wiki.t1/362880 
set Wiki.cosa to 1 - Wiki.t2/2 + Wiki.t2*Wiki.t2/24 - Wiki.t6/720 + Wiki.t6*Wiki.t2/40320
set Wiki.tana to Wiki.sina/Wiki.cosa

Arcsine - Abramowitz/Stegun Approximation

Abramowitz and Stegun found this polynomal approximation for arcsine:

a0=1.5707288 / a1=-0.2121144 / a2=0.0742610 / a3=-0.0187293

arcsin(x) = 180/Pi * (pi/2 - sqrt(1 - x) * (a0 + a1*x + a2*x^2 + a3*x^3))

This function requires the following variables to be declared in your Global Script: 

float x (the sine of the angle)
float n (used internally)
float arcsinx (the arcsine, that is, the measure of the angle)

These may be renamed, but doing so means changing them in the code. 

; script originally by JOG
set Wiki.x to (player.getpos z - NPC.getpos z)/player.getdistance NPC
set Wiki.n to 1 - Wiki.x ; arcsinx = SquareRoot(1-x)
set Wiki.arcsinx to Wiki.n/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.arcsinx to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2
set Wiki.n to (Wiki.arcsinx+(Wiki.n/Wiki.arcsinx))/2

set arcsinx to 57.2957795*(1.5707963-Wiki.n*(1.5707288-0.2121144*Wiki.x+0.0742610*Wiki.x*Wiki.x-0.0187293*Wiki.x*Wiki.x*Wiki.x))

This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations.

Arcsine - Approximation by Taylor Series

According to Wikipedia, arcsine can be found with this series:

Arcsine.png

This can be approximated by Oblivion using a function. This function requires the following variables be declared in your Global Script: 

float z (the sine of the angle)
float z3 (used internally)
float z5 (used internally)
float z7 (used internally)
float arcsinz (the arcsine, that is, the measure of the angle)

These can be renamed, but must also be changed in the code. 

;script originally by DragoonWraith
set Wiki.z3 to (Wiki.z*Wiki.z*Wiki.z)
set Wiki.z5 to (Wiki.z3*Wiki.z*Wiki.z)
set Wiki.z7 to (Wiki.z5*Wiki.z*Wiki.z)

set arcsinz to (Wiki.z+(1/2)*(Wiki.z3/3)+(3/8)*(Wiki.z5/5)+(15/48)*(Wiki.z7/7))

More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit.


Arccosine

Arccos z = (PI / 2) - arcsin(z).

See above for method of obtaining arcsin. This may be useful when using the Law of Cosines to find the measure of an unknown angle, given three known sides.


Arctangent

Arctan z = z - (z^3/3) + (z^5/5) - (z^7/7) +...

This is very similar to the Taylor Expansion method of generating Arcsine, but without the extra multipliers, and with alternating signs.

This function requires the following variables be declared in your Global Script: 

float z (the tangent of the angle)
float z3 (used internally)
float z5 (used internally)
float z7 (used internally)
float arcsinz (the arctangent, that is, the measure of the angle)

These can be renamed, but must also be changed in the code. 

;modified from arcsine script supplied by DragoonWraith
  set z3 to ( z * z * z )
  set z5 to ( z3 * z * z )
  set z7 to ( z5 * z * z )

  set arctanz to ( z - (z3/3) + (z5/5) - (z7/7) )

Again, more terms equals more accuracy.

See Also

Elder Scrolls Forums - Trigonometry Function Workarounds?

Elder Scrolls Forums - Is there an actor for the target you are attacking currently?

Retrieved from "https://cs.uesp.net/w/index.php?title=Trigonometry_Functions&oldid=32345"