This is a repository of functions used in trigonometry - namely Sine, Cosine, Tangent, Arcsine, Arccosine, and Arctangent.

There are many methods of obtaining any or all of these, and each has its own benefits and drawbacks in terms of length, efficiency, and speed. This page is a work in progress - please add any scripts you have for approximating these functions. Please remember to comment them thoroughly and to use generic variable names.

Formulae

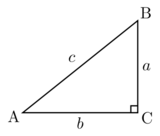
A + B + C = 180°

A + B = 90°

a² + b² = c²

sin(A) = a / c

cos(A) = b / c

tan(A) = a / b

tan(A) = sin(A) / cos(A)

Sine, Cosine, and Tangent

You can use a Taylor series to approximate the value of sine, cosine and tangent:

sin(x) = x^1/1! - x^3/3! + x^5/5! - x^7/7! + ...

cos(x) = x^0/0! - x^2/2! + x^4/4! - x^6/6! + ...

tan(x) = x^1/1! + x^3/3! + x^5/5! + x^7/7! + ...

Taylor Series Variant 1

ScriptName SineCosineTangent
; script originally by Galerion

float ang
float rad
float cos
float sin
float tan
float exp

Begin {appropriate blocktype}

; how one sets ang depends on implementation. Here it is the player's Z rotation
  set ang to Player.GetAngle Z

; normalize angle
  if ( ang < -180 )
    set ang to ( ang + 360 )
  elseif ( ang > 180 )
    set ang to ( ang - 360 )
  endif

; approximate sine and cosine of the angle
  set rad to ( ang * 0.0174533 )
  set cos to 1
  set exp to rad                     ; 1st
  set sin to exp
  set exp to ( exp * rad )           ; 2nd
  set cos to ( cos - exp / 2 )
  set exp to ( exp * rad )           ; 3rd
  set sin to ( sin - exp / 6 )
  set exp to ( exp * rad )           ; 4th
  set cos to ( cos + exp / 24 )
  set exp to ( exp * rad )           ; 5th
  set sin to ( sin + exp / 120 )
  set exp to ( exp * rad )           ; 6th
  set cos to ( cos - exp / 720 )
  set exp to ( exp * rad )           ; 7th
  set sin to ( sin - exp / 5040 )
  set exp to ( exp * rad )           ; 8th
  set cos to ( cos + exp / 40320 )
  set exp to ( exp * rad )           ; 9th
  set sin to ( sin + exp / 362880 )

; get tangent
  set tan to ( sin / cos )

End

This can be placed within your own code or run as a separate script and checked by yours (though the former is probably easier). The sin, cos, and tan variables are your outputs, ang is your input.

This script is more accurate than it needs to be. Galerion suggests that only the first seven steps are necessary.

Taylor Series Variant 2

ScriptName SineCosineTangent
; script originally by JOG

float angle ; Input
float sina  ; Output Sin
float cosa  ; Output Cos
float cosa  ; Output Tan
float t1
float t2
float t5
float t6

Begin {appropriate blocktype}

  set angle to player.getangle z
  if angle < -180
    set angle to angle + 360
  elseif angle > 180
    set angle to angle - 360
  endif

  set t1 to angle / 57.29577951    ; precalculate powers of "angle"
  set t2 to t1*t1 
  set t5 to t2*t2*t1
  set t6 to t5*t1
  set sina to t1 - t1*t2/6 + t5/120 - t5*t2/5040 + t6*t2*t1/362880 
  set cosa to 1 - t2/2 + t2*t2/24 - t6/720 + t6*t2/40320
  set tana to sina/cosa
end

Arcsine, Arccosine, and Arctangent

Sin=Opp/Hyp - The arcsine is the angle between two points, when the distance is the hypotenuse of the triangle and the opposing side is either the x- or the y-difference (whatever is shorter). To get the z-angle (left/right) between two objects in Oblivion you can use the function GetHeadingAngle. But when you need the x-angle (up/down) you still have to calculate the arcsin.

Arcsine - Abramowitz/Stegun Approximation

Abramowitz and Stegun found this polynomal approximation for arcsine:

a0=1.5707288 / a1=-0.2121144 / a2=0.0742610 / a3=-0.0187293

arcsin(x) = 180/Pi * (pi/2 - sqrt(1 - x) * (a0 + a1*x + a2*x^2 + a3*x^3))

scriptname Arcsine 
; script originally by JOG
   
float x        ; Input  (Sine)
float arcsinx  ; Output (Angle)
float n

Begin {appropriate blocktype}
 set x to (player.getpos z - NPC.getpos z)/player.getdistance NPC
 set n to 1 - x                           ; arcsinx = SquareRoot(1-x)
 set arcsinx to n/2
 set arcsinx to (arcsinx+(n/arcsinx))/2
 set arcsinx to (arcsinx+(n/arcsinx))/2
 set arcsinx to (arcsinx+(n/arcsinx))/2
 set n to (arcsinx+(n/arcsinx))/2

 set arcsinx to 57.2957795*(1.5707963-n*(1.5707288-0.2121144*x+0.0742610*x*x-0.0187293*x*x*x))
End

This approximation is very accurate (99.9% - 99.9999%) for angles of 45 degrees and higher. For smaller angles you can get a higher precision when you use a taylor series with 15+ iterations.

Arcsine - Approximation by Taylor Series

According to Wikipedia, arcsine can be found with this series:

This can be approximated by Oblivion using the following script:

scriptname Arcsine
;script originally supplied by DragoonWraith

float z
float z3
float z5
float z7
float arcsinz

Begin {appropriate blocktype}

;z can be set depending on implementation
;here it is set to the number of places discovered by the player
;(a completely bizarre thing to find the arcsine of)
  set z to GetPCMiscStat 7
  set z3 to ( z * z * z )
  set z5 to ( z3 * z * z )
  set z7 to ( z5 * z * z )

  set arcsinz to ( z + (1/2)*(z3/3) + (3/8)*(z5/5) + (15/48)*(z7/7) )

End

More terms will increase accuracy. The larger the angle, the more terms are needed to get acceptable accuracy. As a rough guide use 3 terms for every 10° to get an accuracy of at least 1 decimal digit.

Arccosine

Arccos z = (PI / 2) - arcsin(z).

See above for method of obtaining arcsin. This may be useful when using the Law of Cosines to find the measure of an unknown angle, given three known sides.

Arctangent

Arctan z = z - (z^3/3) + (z^5/5) - (z^7/7) +...

This is very similar to the Taylor Expansion method of generating Arcsine, but without the extra multipliers, and with alternating signs.

scriptname Arctan
;modified from arcsine script supplied by DragoonWraith

float z
float z3
float z5
float z7
float arctanz

Begin {appropriate blocktype}

;z can be set depending on implementation
;here it is set to the number of places discovered by the player
;(a completely bizarre thing to find the arcsine of)
  set z to GetPCMiscStat 7
  set z3 to ( z * z * z )
  set z5 to ( z3 * z * z )
  set z7 to ( z5 * z * z )

  set arcsinz to ( z - (z3/3) + (z5/5) - (z7/7) )

End

Again, more terms equals more accuracy.

Trigonometry Functions

Contents